(1)Numerous research related to physico-chemical transformations in atmosphere discuss specificity of the processes going under effect of the solar radiation, electric discharges and other factors [1-12]. However, a range of phenomena have not found a theoretical explanation based on exact calculations or experimental data yet.
This work is focused on studies of the phenomena related to the high-temperature chemical processes happening in the intensive atmospheric fields, i. e., basically, to the ball lightning phenomenon*. The key objective of this study is to demonstrate that the ball lightning can be a diffusional flame maintained by the atmospheric d. c. currents.
* An identified flying object observed by the author, in March,
1980, 4p. m., at a site near Moscow in low continuous cloudiness (temperature
about 0oC). The object was observed over the forest, at distance some
70-IOO m away, at altitude of 50-80 m. The object remained motionless and was
observed for over 15 minutes. It hardly looks like a typical ball lightning.
However, the object image resembles quite much the ball lightning photograph
taken by Charman W. N. (New Scientist, 56, 1972, p. 632).
The thermodynamic and kinetic analysis results [13-14] make it possible to single out the basic chemical reactions going on in the lightning storm atmosphere as well as the high-temperature ionization processes shaping the ball lightning phenomenon.
Firstly, let's discuss the specific features of the physico-chemical transformations of the lightning storm air in a wide temperature range. In the lightning storm atmosphere nitrogen oxides, ozone and other "combustible" components start to accumulate reaching concentrations in excess of the normal levels (sometimes by several tent olds). Thus, nitrogen oxide is synthesized through -the following process:
(1)where: the reaction heat effect 
relates to standard conditions. Having entered the
low-temperature zone, 
is "tempered" [15,16] and can react with oxygen and ozone as in
the below equations:
(2)
(3)Under the lightning storm conditions the processes described by the cumulative equation of the below type become significant too:
(4)The created 
dissociates in rain drops and fog particles in the following
way:
(5)It should be noted that 
, also a product of the cumulative process, is similarly
unstable even at low temperatures and in the liquid phase decomposes
into 
and 
. In addition, there are other known processes of the type:
(6)
(7)increasing the liquid phase conductivity by several orders. The reactions
of 
and 
decomposition in the gaseous phase under the appropriate
conditions can generate some amounts of ions as well.
Considering the ionization potentials and the values of affinity to electron
and proton of the particles identifiable in the atmosphere, one can state that
at temperatures of 300-500K the atmospheric air contains 
and some other ions in relatively increased concentrations.
However, it should be noted, that due to the kinetic and thermodynamic
limitations as well as to the specificity of the nitrogen based oxygen
compositions chemistry, the ion composition in the atmospheric air under effect
of temperature changes can vary in the real environment in a complex manner
(e.g. reaction 1 in the above range has some kinetic limitations; 
can withstand temperatures practically up to 900K,
whereas thermal decomposition of 
is noticeable at 800K and above, etc.).
The most significant role in the charged, particles generation in the atmosphere is probably played, by the relatively advantageous, in terms of thermodynamics, ionization processes involving electron transfer. Thus, e. g. Interactions:
5.4
eV (8)
5.3
eV
(9)
5.9
eV
(10)
eV
(11)can intensively proceed, in the atmosphere including the lightning discharge area, and roles of different reactions can vary depending on the temperatures (at the right hand. side of equations 8-10 the upper possible values of the processes' heat are indicated, whereas the lower limit values are given in brackets).
The mentioned above ions are easily registered in the atmosphere and ionospheres of planets [9-17]. However, it has been often mentioned that the ion concentrations are significantly higher than those calculated by the Saha-Boltzman equation [18-20]:
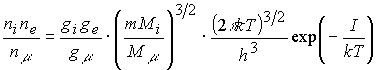(I)because the equation was obtained assuming that the thermal ionization of atoms and molecules (A) in the system goes in the spontaneous way only
(12)and the electric ionization and. other ionization processes on surfaces of
solid particles always present in the atmosphere are not accounted for. In
relation (1) the following symbols are used: 
- concentrations of ions, electrons and neutral atoms or
molecules; 
- corresponding statistic weights; 
- masses of the particles; 
- ionization potential.
For example, comparison of the experimental values of ion concentrations in
the lightning storm atmosphere (containing fivefold excess of 
) at 1000K as well as those in the corresponding flame
zones, against the values calculated using the Saha equation assuming even the
abnormally low mean value of 
= 6 eV, shows that the experimental data exceed the calculated
values by several orders.
On the other hand, the experimentally defined values of n. in the lightning
storm atmosphere correlate well with the estimates obtained by extrapolation of
the experimental data on transformation of the oxygen compositions of nitrogen
in liquid media with a low dielectric permittivity where effective dissociation
of the above compositions is observed with generation of 
ions [21-23]. This is yet another evidence of the solvatational
and other effects role in dissociation in the real atmospheric environment.
Thus, we come to the conclusion that calculations by Saha assuming only
process (12) going on at temperatures about 1000K for the real atmosphere give
significantly underestimated values of 
.
However, the theoretical values of determined using formula (I) for the air at temperatures
2000-2500K should have a better correlation with the experimental data. The fact
is that under such temperature the type (12) processes become dominating,
because under the equilibrium conditions the air is practically a mixture of
several gases: 
with higher concentrations as compared to other components (e.
g. 
), and the thermal ionization proceeds using only one component
- 
(with a relatively small ionization potential of 9.267 eV). In
addition, under such conditions the ionization involving solid particles in the
real atmosphere should be small.
Let's now discuss the ball lightning model in general. An electric lightning discharge or a volumetric charge discharge in the atmosphere creates in some point in space an elevated ion concentration and a high temperature, i. e. the conditions required for the ball lightning flame initiation. The flame is of ball (hollow sphere) shape and is maintained by dc atmospheric currents.
Assume that in the relatively cold zones of the sphere the type (2-3)
processes are maintained by diffusion of the "fuel" and oxidants - 
and others.
It can be easily shown that even at the abnormally high concentrations of the
combustible admixtures (about 1 %) and the process mean heat of 35-40Kcal/mole
the heat up can not raise temperature even to 600-700K. The real content of the
combustible products (including 
) in the lightning storm atmosphere in no case can exceed
0.0003% (in volume). Thus, the energy of the discussed chemical processes is by
several levels below the level required for the ball lightning heat up.
Moreover, consideration of a stationary diffusional burning of the fire ball in a stable medium, which in a simplified model can be described by a simple heat transfer and diffusion equations
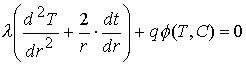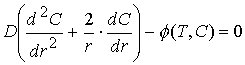(II)
(III)with reasonable assumptions (on small areas of the on-surface transformation
zone, etc.) it easy to establish that this model is unstable against radial
excitations [24]. In equations (II, III): 
- temperature; 
- concentration of combustible matter;
- chemical reaction rate; 
- radial coordinate.
Thus, we understand that is hardly possible to create a purely "chemical" model of the phenomenon without an external energy source.
If some burning gaseous sphere (a ball) containing ions of different polarity
is in the atmospheric electric field, there should be separation of the
on-surface (and volumetric) charges effected in the sphere by the field (as well
as by the thermo-diffusional and other effects though to an insignificant
degree). The charge of such a burning sphere (a ball) and the field intensity on
its surface can be estimated using the known model of field, and model of charge
distribution on a conductive sphere in an external uniform electric field.
Assume, that a sphere of radius 
is positioned in a uniform external electric field of
intensity 
. It is easy to show that the charges on the sphere's surface
are distributed. by the law
(IV)where: 
- on-surface charge density; 
- polar angle; 
-dielectric constant. Such a distribution of charges is
characterized by the dipole moment
(V)where: 
- element of area; 
- radial coordinate; 
- unit vector along z axis in the 
field direction. The electric field beyond the sphere is defined
as
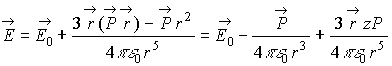(VI)It should be noted that the ball's own electrostatic field intensity, the
charge of which is uniformly distributed over the ball surface, coincides beyond
the ball limits with the point charge intensity, 
, positioned in the ball center. It is hard to say to what
degree of approximation the ball lightning can be treated as a burning sphere.
It may well be closer to burning ball charged uniformly over all volume.
However, at the phenomenon principle model creation it does not matter which of
the cases is realized in nature (it is not excluded that the both ones). So,
let's estimate density of the conductivity current, 
, for the "droplet" case
Ñ 
(VII)where: 
- conductivities of the positive and negative
ions; - potential (
Ñ ).
Using relation (VII) let's estimate density of the conductivity current for
the realistically possible values of the ion concentrations, 
, potential gradient 
(Ñ )in the lightning storm atmosphere at temperature of 2500K.
Selection of this temperature value is fairly well substantiated because the
ball lightning temperature varies in a wide range and as a rule should reach
this selected, value.
Assuming = 109
ion/cm3, ion mobility 
= 50cm2/s× V, We obtain 
= 7 103 s-1, where: 
- charge of electron (4.8× 10-10 CGSEq). Further, taking into
consideration that in the pre-discharge instance | 
| of the linear lightning can be equal
to 104 V/cm2,
the value of in the "droplet" is 10-4
A/cm2. Note, that the same density
of current is obtained, at
n. = 1010 ion/crn3
and | | = 103
V/cm, etc.
The obtained value of current is quite adequate to observe the
diffusion-limited endothermic synthesis (1) and to maintain the gaseous ball
(sphere) at a temperature of many hundred degrees. The obtained estimates
correlate well with the theoretical analysis and other calculation data. It can
be shown that the model of the diffusionally controlled reaction in the sphere
(burning, synthesis, etc.) maintained by 
current of power below the break down threshold is similar to
"burning" of the spherically symmetrical optical charge [14-20] and is stable
against radial excitations.
Inflow of current heats up the sphere providing for synthesis as it has been mentioned above. Additional quantities
of nitrogen oxide can be generated by the electric synthesis associated with the
reactions of the below type
(13)
, and
other
(14)Synthesis of 
and other products [25] can go in the relatively cold areas of
the sphere and its adjacent environment.
Reaction (1) has been studied quite well; 
and 
of the process are known. Hence, from equation
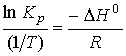
it is easy to calculate the reaction coefficient 
and., correspondingly, concentration in the equilibrium mixture at the given
temperature. Further, by putting the 
concentration value into the Saha equation (1) it is possible to
estimate ionization level using relation [20]
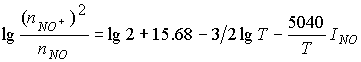(VIII)E. g., using values of 
= 9.276 eV, 
= 3.60 10-3 = 2500K, 
= 7× 1016 particles/cm (2.4 % by volume, by some other data - 2.0
%), we obtain 
4.2× 109 particles/cm3.
Hence, it is evident that at 2500K the calculation gives a very high value of
ion concentration. The true ion concentration, as it has been mentioned, above,
can be even somewhat higher. Such an ion concentration, as it has been discussed
earlier, provides for flow of current adequate to maintain endothermic burning
and to heat up the ball of lightning. Note, that for T = 2000K: 
= 3-1016
particles/cm3 and 107 which corresponds to the
current some two orders lower as compared to the current at 2500K.
The lightning heat is transferred into environment, and the temperature
inside the ball is distributed in the quasistationary way. let's consider a
simplified model of the gaseous ball ("droplet") in which the energy, 
, is emitted due to the electric current passage. The
value of is equal to the Joulean heat minus the reaction endothermic
heat.
For the spherically symmetric problems the stationary equation of heat
conductivity at presence of a heat source with power density of 
is given in the form of
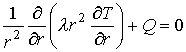(IX)where: 
- heat conductivity; 
- radius. Solution of equation (IX) for the ball interior has
the form of
(X)where: 
- temperature at the ball-air boundary; - the ball radius; 
- temperature at distance from the ball center.
Assuming that - quantity of heat generated in the conductive medium of the
lightning ball and is determined by the Joule-Lenz law
where: 
- current (ampere); 
- voltage (volt); 
- time (second). Given that 
= 4 10-5 A/cm2,½ Ñ ½ = 104
V/cm, we get = 9.6.10-2 cal/cm3 s. Further, at = 300K, = 8-10-4 cal/cm× s× K, and 
= 10 cm, we get the temperature value at the ball center equal
to 2300K, and the temperature 1 cm away from the ball surface 680K.
To present this in a more obvious way, estimation of the air molecules
diffusion time, 
, i. e. time for the air molecules diffusion into the sphere
with = 10 cm at mean temperature of 2000K (
, where 
- diffusion coefficient), easily shows that the quantity of the
heat absorbed in the course of the diffusion-limited reaction (1) is a small
fraction (about 1 %) of the q value required for the sphere heat up. Thus, for
the model being discussed, is consumed actually for the gaseous ball heat up only.
The quantitative evaluations listed above lead us to the conclusion that
under the real conditions the atmospheric volumetric charges pass through the
ball lightning and maintain it. Our approach in terms of the phenomenon physics
correlates with the findings discussed in some other publications [4,26-29]
considering the possibility of the transversal "compression" of the
cloud-to-ground current (equation IV) in the high conductivity area., and
noting that the ball (sphere) positioning into a atmospheric field 
triples field intensity in the sphere. However, it should be
noted that the above mentioned and other studies have not paid the proper
attention to the specific role of the atmospheric volumetric charges (discharge
between which in no way can be connected neither to thunderclouds nor to the
ground), and have not offered a realistic physico-chemical mechanism of ion
formation and maintenance of high concentrations of charges in the ball
lightning. Disregard to the "chemistry of the phenomenon" has, probably, led a
number of authors to overestimation of the temperatures in the ball of
lightning.
As it has been widely known, quite strong horizontal atmospheric currents are able, to our estimates, to maintain the ball lightning. Those currents are especially high when volumetric charges are generated at the lightning storms, fogs, smogs, snow storms, dust storms. Those charges can maintain burning of the ball lightning same as they can induce illumination of electric bulbs [26].
Decrease of voltage and current in the atmosphere causes the ball lightning
death (disappearance). However, at the critical discharge values (in a lightning
storm) an explosion may happen or a linear lightning discharge (sparkle, arch)
with an enormous amount of energy release - the ball lightning dies in the
explosion. It is evident, that though the ball lightning has a relatively small
stock of interior energy, it can initiate high energy discharges in the
atmosphere. In principle, there is yet another possibility of a ball lightning
death - a local explosion of a "chemical nature" with no discharge of a
significant power- the energy of such an explosion is relatively small. It
should be noted, that analysis of I, VI, X type equations shows that a stable
regime of burning in the lightning can be obtained by variation of some
parameters (
, etc. ) in a narrow range. The bulk of those parameters are
interrelated. It is clear now why the ball lightning is such a rare phenomenon
with such a short lifetime.
A more detailed theory of the phenomenon can be developed with regard to the general approaches to the heat explosions and to the break down of dielectrics [30,31] in the similar way as it has been applied to other processes [32-34].
The model developed by us, though doesn't account for some factors (e. g. convective transfer of matter, electric ionization degree, energy loss at irradiation, side reactions in the cold zones, etc.), is basically substantiated with reliable experimental data and is capable to explain many specific features of creation, behaviour and death of both the ball lightning and. the unidentified objects [11]. The proposed model can be easily checked experimentally. A number of concepts quoted in this study have been offered by some researchers earlier. However, the existing theories, as a rule, have not been substantiated with the real chemistry of the lightning storm atmosphere and account for only individual aspects of the phenomenon being discussed (either only physical or desciptional chemical ones, etc.). The authors of the theories have not offered any physico-chemical mechanism of ion formation and. maintenance of the required charge concentration in the ball lightning. Our model explains a range of the known facts and. concepts and actually presents a detailed physico-chemical model of the phenomenon.
The proposed, model doesn't in principle contradict to many well known data and new findings as well as to calculations by various authors [35-38]. It is quite probable that the ball lightning phenomenon is associated with the mechanisms of the processes that have not been discussed in this paper. However, the author believes that the ball lightning is indeed a diffusional flame fed by external energy source. The ball lightning may well be considered as similar to the plasma flame created at combustion of nitrogen in industry at the nitric acid. production.
References.
1. Chalmers, J. A. , Atmosphernoe electrichestvo, Gidromet. izd. , L., 1974.
2. Shishkin, N. S., Oblaka, osadki i grozovoe electrichestvo, Gidromet. izd,, 1964, 401 p.
3. Singer, S., The Nature of Ball lightning, New York - London, Plenum Press, 1971.
4. Uman, M. A., lightning, McGrow-Hill, New York, St. Sowis, San Francisco, Toronto, Sidney, 1969 (Russian translation MIR publishers, M., 1972, 328 p.).
5. Frenkel, Ya. I., Teoria osnovnykh yavieniy atmosphernogo elevtrichestva, lzv. AN SSSR, ser. geogr. i geofiz., 8, No. 5, 244-272, 1944.
6. Nauer, H., Z. Phys. , Modellversuche zum Kugelblitz, 5, No. 12 , 1953, 441-450 pp.
7. Veitsekhovskiy, B. B., Ogni Elma i svechenie na predmetakh v oblake electricheski zaryazhennykh kapel vody, DAN SSSR, 262, No. 1, 1982, 84-88 pp.
8. Sutugin, A. G., Petryanov, 1. V. , Khimicheskie prevrascheniya okislov ugleroda i azota v almostere, Fizika almosfery, No. 2, 28-33, Vilnus.
9. Khrgian, A. Kh., Kuznetsov, G. 1., Problema nablyudeniy i issledovaniy atmosphernogo ozona, Izd. MGU, 1981, 216 p.
10. Elanskiy, E. P., Trutce, Yu. L., Nekotorye osobennosti raspredeleniya obschego soderzhanlya ozona i dvuokisi azota v atmosfere, Izd. AN SSSR, Fizika atmosfery i okeana, 15, No. 1, 119-121, 1979.
11. Crew, E. W., Meteorological Flying Objects, Q. H. R. Astr. Soc., 21, 216-219, 1980.
12. Singer, S., Ball lightning, Naturwissenschaften, 67, 332-337, 1980.
13. Gurvich, 1. V., Karachevtsev, G. V., Kondratjev, V. N., Lebedev, Yu. A., Medvedev, V. A., Potapov, V. K., Khodeev, Yu. S., Energiya razryva khimicheskikh svyazei. Potentsialy ionizatsii i srodstvo k electronu, M., Nauka, 1974, 351 p.
14. Virin, L. 1., .Dzhagatspan,yan, V. V., Karachevtsev, G. V., Potapov, V. K., Talrose, V. li., lonno-moleculyarnye reactsii v gasakh, M., Nauka, 1979, 548 p.
15. Zeidovitch, Ya. B., Barenblatt, T. 1., lailrovitch, V. B., Makhviladze, G. M., Matematicheskaya teoriya goreniya i vzryva, M., Nauka, 1980, 478 p.
16. Zeidovitch, Ya. B., Sadovnikov, P. Ya., Frank-Kamenetsky, D. A., Okisleniye azota pri gorenii, lzd. AN SSSR, M., L., 147 p.
17. Bauer, Z., Fizika planetnykh ionospher, M., MIR, 1976, 251 p.
18. Raizer, Yu. P., Osnovy sovremeniloy fiziki gazorazryadnykh processov, M., Nauka, 1980, 416 p.
19. l.auton, J., Vainberg, F., Electricheskie aspecty goreniya, M., Energiya, 1976, 294 p.
20. Lieng, K., Astrofizicheskie formuly, chast I, M., MIR, 326-331 p., 1978.
21. Goddard, D. R., Hughes, E. D., Ingold, C. K., J. Chem. Soc., 2539, 1950.
22. Usanovitch, M. 1., Issledovaniya v oblasti teorii rastvorov i teorii kislot i osiiovaniy. Izbrannye tru.dy. Alma-Ata, Nauka, 1970, 363 p.
23. Gladyshev, G. P., Fiziko-khimicheskoye issledovanie nekotorykh sistem, soderzhaschikh azotnuyu i sernuyu kisloty, Alma-Ata, Kaz, GU, 1959, 124 p.
24. Selezneva, 1. K., Sfericheski simmetrichny opticheskiy razryai kak analog diffusioruiogo goreniya v smesi goryuchikh gasov, In: Goreniye i vzryv, M., Nauka, 396-400, 1972.
25. Filippov, Yu. V., Electrosintez ozona, Vestnik MGU, No. 4, 153-186, 1959.
26. Tverskoy, P. N., Atmosphernoye electrichestvo, L., Gidromet. izd., 1949, 252 p.
27. Firikelstein, D., Rubinstein, J., Ball lightning, Phys. Rev., 135, 2A, 390-396, 1966.
28.Andersen, W. H., Energy Source for Ball lightning, J. Geophys. Res., 70, 6, 1291-1293, 1965.
29. Uman, M. A., Helstrom, C. W., A Theory of Ball Lightning, J. Geophys. Res., 71, 8, 1975-1984, 1966.
30. Semenov, N. N., K teorii kinetiki khimicheskikh reaktsiy, J. Rus. fiz. -khim. obschestva, 50, No. 6, 533-537, 1928.
31. Fok, V. K., K teplovoy teorii electricheskogo proboya, Tr. Leningr. fiz. -tekhn. laboratorii, 5, 52-71, 1928.
32. Velikhov, E. P., Dykhne, A. M., In: "Trudy VII Simpoz. po ioniza tsionnym yavieniyam v gazakh, Belgrad, 1967, p. 47.
33. Merzhanov, A. G., Rumanov, E. N., Teplovye processy tipa goreniya v fizike. Preprint IKHF AN SSSR, Chernogolovka, 1975, 21 p.
34. Fristrom, R. M., Vestenberg, A. A., Struktura plameni, M., Metallurgiya, 1969, 363 P.
35. Stakhanov, 1. P., 0 fizicheskoy prirode sharovoy molnii, M., Atomiziiat, 1985.
36. Smirnov, B. M., Priroda, 1987, No. 2, p. 15-26.
37. Smirnov, B. M., Problema sharovoy molnii, M., 1987.
38. Barry, James S., Ball lightning and Bead Lightning, Extreme Forms of Atmospheric Electricity, N. Y.,L., Plenum Press, 1980 (Russian translation: M., MIR, 1983, 288 p.).